Steam Technologies is a service provider which uses strictly steam-powered computers. They have recently developed a new type of oracle taking advantage of the steam-power architecture. They offer a huge price in case someone decrypts the message from their service. Are you up for the challenge?
Category: crypto
Solver: n1k0, nh1729
Flag: HTB{m4ng3r5_4tt4ck_15_c001_4nd_und3rv4lu3d}
Writeup
We need to decrypt an RSA ciphertext and for that we are provided with the ciphertext, the public key, and an oracle. We can query the oracle with ciphertexts, it decrypts them with the private key belonging to the provided public key, and then responds with the byte length of the decrypted message.
The padding and the oracle reminds us of the Bleichenbacher Attack [1], but while we have indeed PKCS #1 padding, the oracle is a bit different. So we first try to come up with some fancy solution of our own, inspired by the Bleichenbacher Attack.
We know that we can exploit the malleability of RSA to create valid ciphertexts for m' = m * s mod N for arbitrary values of s chosen by us. For that we just need to calculate c' = c * s^e.
Now we get the byte length L of m*s mod N and can therefore learn the following:
2^(8*(L-1)) <= ms mod N <= 2^(8*L) - 1
As we were not able to deduce information about the interval for m with that, we tried to better understand how the Bleichenbacher Attack uses the learned information to define an interval for m. We did not understand this from the paper, so we looked for code. While searching for Bleichenbacher Attack code, we stumbled upon some other attacks against PKCS #1 padding in a public GitHub repo [2]. The oracle that is used in the Manger attack [3] looks quite similar to the one we have in our challenge.
Next, we test the code we found and modify it, so that it communicates with the remote oracle. We receive public key and ciphertext from the challenge and next we perform the Manger attack on these. For each oracle request, we encode the number as bytes/hex, send it over, and parse the response. With that, the attack runs through and it steadily shrinks the possible interval.

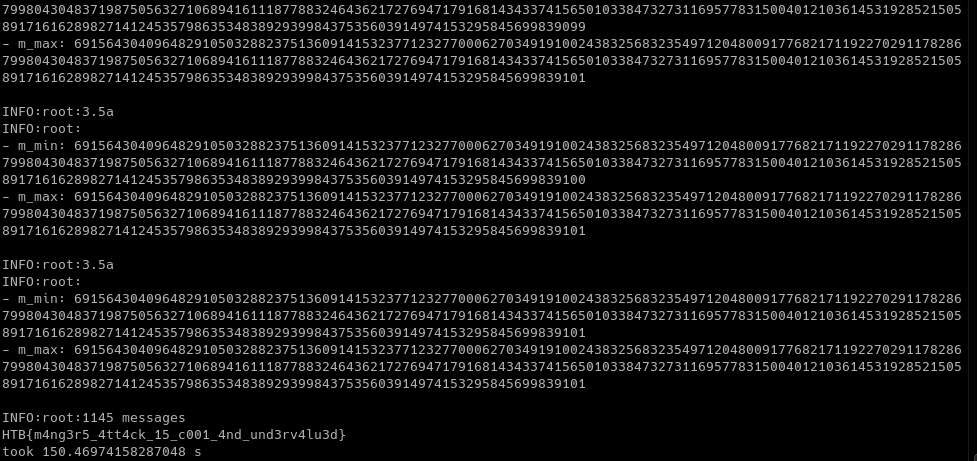
Finally, after about 1,100 oracle requests and two and a half minutes, the range for m is shrunken to only a single value. In byte representation we see that the message contains some padding followed by the flag.
b'\x02Z\xeb\x83)\xa1\x8f\xa3\x90\x19\xc5}\xb2\xdd&7$\xa8@\xb1fS\xf5\x0eGP\xa1\xf1\xf0\x97\xaf+\x14"/\xf7\x8b\x97\x1c\x10\xbaA\x89|\xe1b\x1f\x06m\xe7\xde\xb9\x18\xfa\xfd\xe5\xd6;6\x9dm\x0b&\xe9\xfd\xcc!\xe2\x1a\xcd\x8b\xefnI\rC6\xdc8\x9a\x8b\x13\xcb\x00HTB{m4ng3r5_4tt4ck_15_c001_4nd_und3rv4lu3d}'
We strip the padding away and print out the flag.
Other resources
[1] https://link.springer.com/content/pdf/10.1007%2FBFb0055716.pdf
[2] https://github.com/mimoo/RSA_PKCS1v1_5_attacks
[3] https://link.springer.com/content/pdf/10.1007/3-540-44647-8_14.pdf