Our domain has been attacked. An APT group has taken over our server and they have locked us out. Our incident response team was able to find some files added on the upload directory but havent been able to extract any information from them. Could you help us login back?
Category: crypto
Solver: Miroka, HTTP418, kh1
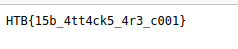
Flag: HTB{15b_4tt4ck5_4r3_c001}
Writeup
What we got
- encryption.py - the script used to encrypt the new password
- leaks - the script’s variables n, rp, and rq
- new_password - the encrypted new password
encryption.py resembles RSA encryption with two primes p and q that are slightly above square numbers and the variables rp = 228 and rq = 75 tell us, how much above. We have also given the implicit RSA-e-Variable of the public key as it is a constant in the encryption.py.
unknown variables: x ~ 512 bit, y ~ 512 bit, d
p = x^2 + rp ~ 1024 bit
q = y^2 + rq ~ 1024 bit
n = p * q ~ 2048 bit
We recognize that p and q are slightly above square numbers.
Our task is to calculate a matching private key for the given public key <e=65537, n=........>.
How to attack it
The weakness of this public-key n is that it is the product of two numbers that are slightly above square numbers. Therefore, n is also slightly above square numbers:
n = p * q
n = (x^2 + rp) * (y^2 + rq)
n = (x * y)^2 + rq * x^2 + rp * y^2 + rq * rp
n ~ 2048 bit
n ~ (~512 bit * ~512 bit)^2 + 2*(~512 bit)^2 + (~0 bit)
n ~ (~1024 bit)^2 + (~512 bit)^2
n ~ (~2048 bit) + (~1024 bit)
n ~ 2048 bit
Let’s show why we can (nearly) ignore a 1024-bit number. We know that n is slightly above a square number. The difference between two successive square numbers can be calculated as follows (let a be a natural number):
(a + 1)^2 = a^2 + 2*a + 1
(a + 1)^2 - a^2 = 2*a + 1
As a consequence, in such number regions as our n is in (~2048 bit), successive square numbers have a difference of roughly ~1025 bit. This insight makes it obvious, that we can nearly ignore the secondary addend that produce our n and we can focus on the (x * y)^2 part.
The simple consumption would that x * y equals the integer square root of n, but this would be too simple, because then we would underestimate the other (still existing) secondary addends. Therefore, the following must be true:
Let i be a small positive number.
x * y = isqrt(n) - i
Now we have two formulas with two completely unknown variables (x and y) and one partially known variable (i):
n = (x^2 + rp) * (y^2 + rq)x * y = isqrt(n) - i
This equation system can be solved by testing different values for i.
How we break it
We got two formulas for every value of i that we must automatically solve. Sympy (Python) can do this job well:
import sympy, math
n = ...
rp= 228
rq= 75
n_sqrt = math.isqrt(n)
x, y = sympy.symbols("x y", real=True)
eq1 = sympy.Eq(n, (x*y)**2 + x**2 * rq + y**2 * rp + rq*rp)
for i in range(1000):
eq = Eq(x*y, n_sqrt - i)
solution = solve([eq2, eq], [x,y], domain=S.Naturals)
if len(solution) > 0:
print(i, solution)
break
For i = 144 we get 4 solution pairs of which only one pair consists of natural numbers, so we found x and y.
Using those, we can now calculate and check p and q:
p = x**2 + rp
q = y**2 + rq
n == p * q # True
As our wanted private key consists of n and d, we still have to calculate d:
phi_n = (p-1) * (q-1)
d = pow(e, -1, phi_n) # = e^-1 mod phi_n
Now we got our private key and can decrypt the message using the following code:
message = pow(cypher_text, d, n)
print(bytes.fromhex(hex(message)[2:]).decode("utf-8"))
Output: The password is 4p7gr0p0w3ndU
Final Step
Using the decrypted password we can log into our challenge Docker container at http://docker.hackthebox.eu:30905/login using admin as username and 4p7gr0p0w3ndU as password.
Response: Get the flag: HTB{15b_4tt4ck5_4r3_c001}
Fun Facts
The unleeted flag text states lsb attacks are cool, where LSB refers to the least significant bits. It seems like there is a whole class of attacks focusing on partial knowledge about the least significant bits of the primes used for RSA encryption. A quick Qwant search comes up with this paper: A New LSB Attack on Special-Structured RSA Primes. This might be interesting to further look at!