Time for an emoji-test! No need to worry.. You have 500 seconds to answer 100 questions. Five seconds for each question is more than enough! You need to score 100/100 in order to win an amazing prize! Good luck!
Category: misc
Solver: lmarschk
Flag: HTB{3m0j1s_R_fUn_4nd_m4k3_m3_c0d3_f4st}
Writeup
Starting with a telnet connection to the server, we are given a set of questions:
Trying 139.59.202.58...
Connected to docker.hackthebox.eu.
Escape character is '^]'.
You have only a few seconds for each question! Be fast! ⏰
Question 1:
❌ 🌞 🍧 👺 🦄 - 🦄 ❌ 🦄 👺
Answer:
> 123
Time: 2.47
Wrong answer! 😿
The correct answer was 11382
The problem is, that when it is taking too long to get an answer, the connection will be shut down from the server. So there is no possibility to solve this one “by hand”, needing a script in order to do so.
At this point, we suspected that we just have to answer enough of these questions in time in order to get the flag. To get an first impression we pulled several different questions trying to detect a pattern how they are built.
First impression was that the single emojis are single numbers (as we checked with some equations that the magnitude of the result fits more or less). So we needed a mapping of Emoji -> Number in order to calculate (with a little script) the right answer.
We can get such a mapping by building a linear equation system (as some of the terms given by the server are linear). For sake of simplicity, we also used only equations with + as an operator. Now we can map questions from the server to simple equations like this:
❌ 🌞 🍧 👺 🦄 - 🦄 ❌ 🦄 👺 --> 1000*❌ + 1000*🌞 + 100*🍧 + 10*👺 + 🦄 - 1000*🦄 - 100*❌ - 10*🦄 - 👺
As we got several different linear equations, we can build an equation system with (at least) 10 equations, which we can solve then and get the values for the single variables (emojis):
{⛔: 5, ❌: 2, 🍧: 6, 👺: 7, 🔥: 4, 🦄: 9, 🦖: 3, 👾: 8, 🍨: 1, 🌞: 0}
To automate this process (as we were not sure whether these emojis change from time to time), we used sympy to automatically solve the linear equation system.
Attached, you find our scripts emojis_get.py which gets a sample set of questions from the server and writes it as a json file, emojis_find_solution.py, which finds a solution based on those sample questions and emojis_answer.py, which answers the questions to the server based on the generated solution.
With our scripts, it is possible to solve the whole challenge by executing
python3 emojis_get.py | python3 emojis_find_solution.py | python3 emojis_answer.py
which results (at the end of the output) in the following flag:
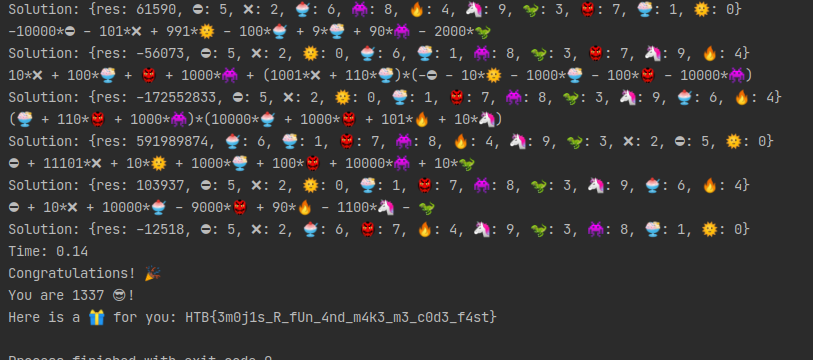
[...]
Solution: {res: 40829, ❌: 2, 🍨: 1, 👾: 8, 🔥: 4, 🦄: 9, 🦖: 3, ⛔: 5, 🌞: 0, 🍧: 6, 👺: 7}
((1010*🍧 + 100*🍨 + 👾 + 10000*🦄)*(10000*🍧 + 👺 + 10*🦄 + 1100*🦖))*(10011*⛔ + 100*🍨 + 1000*👺)
Solution: {res: 348460471889880, ⛔: 5, 🍧: 6, 🍨: 1, 👺: 7, 👾: 8, 🦄: 9, 🦖: 3, ❌: 2, 🌞: 0, 🔥: 4}
-100*⛔ + ❌ - 10000*🍧 + 10*👺 - 10*👾 + 10099*🦄
Solution: {res: 30383, ⛔: 5, ❌: 2, 🍧: 6, 👺: 7, 👾: 8, 🦄: 9, 🍨: 1, 🌞: 0, 🦖: 3, 🔥: 4}
10010*🍧 + 1000*🍨 + 2*🦄 + 1210*🦖
Solution: {res: 64708, 🍧: 6, 🍨: 1, 🦄: 9, 🦖: 3, ⛔: 5, ❌: 2, 🌞: 0, 👺: 7, 🔥: 4, 👾: 8}
Time: 0.14
Congratulations! 🎉
You are 1337 😎!
Here is a 🎁 for you: HTB{3m0j1s_R_fUn_4nd_m4k3_m3_c0d3_f4st}
Scripts
emojis_get.py
import json
from telnetlib import Telnet
import sympy
from sympy import Symbol, linsolve
def get_number(host, port):
with Telnet(host, port) as tn:
# Consume until Question
tn.read_until(b'Question')
tn.read_until(b'\n')
emoji_numbers = []
math_signs = []
current_number = []
while True:
char = tn.read_until(b' ')
char = char.decode('utf-8')
if char == ' ':
continue
char = char.strip()
if char == 'Answer:\n>':
emoji_numbers.append(current_number)
break
if char in ['-', '*', '+']:
emoji_numbers.append(current_number)
current_number = []
math_signs.append(char)
else:
current_number.append(char)
tn.write(b'\n')
tn.read_until(b'The correct answer was ')
correct = tn.read_until(b'\n').decode('utf-8')[:-1]
return emoji_numbers, math_signs, int(correct)
def main():
HOST = 'docker.hackthebox.eu'
PORT = 31141
result = []
for i in range(0, 100):
result.append(get_number(HOST, PORT))
print(json.dumps(result, indent=2))
if __name__ == '__main__':
main()
emojis_find_solution.py
import json
import sys
from telnetlib import Telnet
import sympy
from sympy import Symbol, linsolve
def main():
result = json.load(sys.stdin)
emojis = set()
for run in result:
for word in run[0]:
for emoji in word:
emojis.add(emoji)
equations = []
emoji_var = {}
count = 0
for item in emojis:
# if emoj == ''
emoji_var[item] = Symbol(item)
count += 1
# Just an idea to reduce computational complexity (by a s
# s.append(emoji_var[emoj] >= 0)
# s.append(emoji_var[emoj] < 10)
for run in result:
# To speed up computation by reducing search room significantly
if len(run[0]) > 2:
continue
if run[1][0] != '+':
continue
emoji_numbers = run[0]
math_signs = run[1]
formula = []
word_count = -1
for word in emoji_numbers:
word_formula = None
count = len(word) - 1
for char in word:
char_formula = 10 ** count * sympy.Symbol(char)
if word_formula:
word_formula += char_formula
else:
word_formula = char_formula
count -= 1
if word_count < 0:
formula.append(word_formula)
elif math_signs[word_count] == '+':
formula.append(word_formula)
# Omitted other operations as we are filtering above
else:
raise Exception('Should not happen')
word_count += 1
formula = sympy.Add(*formula)
equations.append(sympy.Eq(formula, run[2]))
solved = sympy.solve(equations[:10], tuple(emoji_var.values()))
print(json.dumps({str(k): int(v) for k, v in solved.items()}, indent=2))
if __name__ == '__main__':
main()
emojis_answer.py
import json
import sys
from telnetlib import Telnet
import sympy
from sympy import Symbol, linsolve
def answer(host, port, sol):
solution_formulas = []
for emoji, value in sol.items():
solution_formulas.append(sympy.Eq(sympy.Symbol(emoji), value))
with Telnet(host, port) as tn:
while True:
tn.read_until(b'\n')
# Consume until Question
tn.read_until(b'Question')
tn.read_until(b'\n')
emoji_numbers = []
math_signs = []
current_number = []
while True:
char = tn.read_until(b' ')
char = char.decode('utf-8')
if char == ' ':
continue
char = char.strip()
if char == 'Answer:\n>':
emoji_numbers.append(current_number)
break
if char in ['-', '*', '+']:
emoji_numbers.append(current_number)
current_number = []
math_signs.append(char)
else:
current_number.append(char)
# This is a hacky way where we could calculate the solution using eval
# result = ''
# word_count = -1
# for word in emoji_numbers:
# word_result = '0'
# count = len(word) - 1
# for char in word:
# word_result = f'{word_result} + {pow(10, count)} * {sol[char]}'
# count -= 1
# if word_count < 0:
# result = f'({word_result})'
# else:
# result = f'{result} {math_signs[word_count]} ({word_result})'
# word_count += 1
# print(result)
formula = []
word_count = -1
for word in emoji_numbers:
word_formula = None
count = len(word) - 1
for char in word:
char_formula = 10 ** count * sympy.Symbol(char)
if word_formula:
word_formula += char_formula
else:
word_formula = char_formula
count -= 1
if word_count < 0:
formula.append(word_formula)
elif math_signs[word_count] == '+':
formula.append(word_formula)
elif math_signs[word_count] == '-':
formula.append(-word_formula)
elif math_signs[word_count] == '*':
formula[-1] = sympy.Mul(formula[-1], word_formula, evaluate=False)
else:
raise Exception('Should not happen')
word_count += 1
formula = sympy.Add(*formula)
print(formula)
result = sympy.solve([sympy.Eq(formula, Symbol('res')), *solution_formulas])
if isinstance(result, list):
result = result[0]
print(f'Solution: {result}')
tn.write(f'{result[sympy.Symbol("res")]}\n'.encode('utf-8'))
response = tn.read_until(b'Correct')
if b'Correct' not in response:
# We got the flag
print(response.decode('utf-8'))
return
def main():
HOST = 'docker.hackthebox.eu'
PORT = 31141
sol = json.load(sys.stdin)
answer(HOST, PORT, sol)
if __name__ == '__main__':
main()